PID

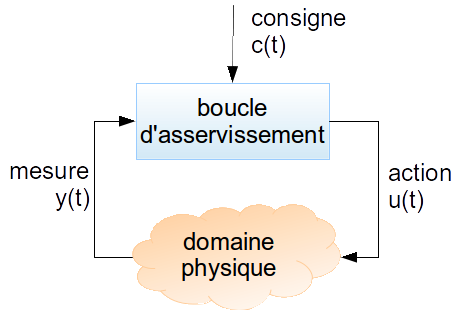
Un processus d'asservissement consiste à réaliser le pilotage d'un système en boucle fermée en relation avec un domaine physique. Il est constitué des éléments suivants, qui sont tous dépendant du temps :

• c(t) – la consigne représente l'objectif à atteindre sur y(t) et est fournie par un sous-système gérant la planification générale de l'action,
• y(t) – permet de mesurer la valeur physique à contrôler et est en général réalisée par des capteurs,
• u(t) – représente l'action sur la grandeur physique et est implanté par un actionneur.

Le processeur d'asservissement consiste à exhiber une fonction f(c(t), y(t)) qui fournie u(t) à chaque instant et assure la convergence de y(t) vers c(t) selon les modalités du problème (convergence rapide, pas de dépassement, etc).

Une solution, actuellement très utilisée, pour cette fonction f est l'utilisation d'un PID (Propertional-Integral-Derivative). Soit e(t), l'erreur, définie par e(t) = c(t) - y(t), on peut exprimer le PID par :

u(t) = Kp e(t) + Ki INT[0 → t] e(t') dt' + Kd de(t) / dt

Avec Kp, Ki et Kd des constantes à définir et propres à un PID donné et INT représentant l'intégration sur le temps.

Les termes de cette formule ont la signification suivante :

• Kp e(t) est la partie proportionnelle à l'erreur et nous la convergence vers c(t),
• Ki INT[0 → t] e(t') dt' est l'intégration de l'erreur sur le temps et permet d'accélérer la convergence,
• Kd de(t) / dt est la dérivé par rapport à l'erreur précédente et permet d'amortir l'arrivé en c(t) pour éviter de l'overshooting.

Le PID fournit un modèle mathématique intéressant mais ne réponde à la question de l'implémentation.

Une première concerne les grandeurs utilisées :

• nos mesures en en °/s ou m/s2 (provenant de l'IMU),
• nos actionneurs sont multiples et pilotés en PWM (période 20ms, 1-2ms pour aller du minimum au maximum).

Comment gérer tout cela ensemble ?

• Les constantes sont là pour ça : elles permettent de paramétrer le comportement du PID mais également de réaliser la conversion entre les différentes unité.
• Choisir sur quelle partie vous allez appliquer le PID : il est même possible de combiner les PID.
• Réaliser un bilan de toutes les unités utilisées.

Comme bilan, on peut remarque que :

• l'IMU donne
  • la vitesse angulaire autour des axes x, y et z (en °/s),
  • l'accélération linéaire sur les axes x, y et z (en m/s2),
• à partir des données précédentes, on peut calculer
  • l'angle de l'appareil par rapport aux axes x, y et z (en °),
  • la position dans l'espace par rapport au repaire (x, y, z) et la position 0 correspondant à la position de départ (en m),
• il faut ensuite savoir quelle est la consigne qui peut être composée,
  • des angles x, y et z recherchés pour l'appareil (en °),
  • de la position x, y, z vers où doit se rendre l'appareil (en m).
• selon cette consigne, il faut régler la vitesse des 4 moteurs
  • avant-gauche (en ms entre 1 et 2),
  • avant-droite (en ms entre 1 et 2),
  • arrière-gauche (en ms entre 1 et 2),
  • arrière-droit (en ms entre 1 et 2).

Cependant, il existe bien des manières de réaliser ce qu'on cherche comme action.

Les deux points un peu compliqué du PID est la programmation de l'intégrale et de la dérivée.

Ces deux termes de calcul dépendent du temps entre 2 mesures, c'est-à-dire de la période de mesure. Dans un monde parfait, l'activation du calcul du PID est précise, c'est-à-dire à la fin de chaque période et le temps dt est égal à la période.

Dans notre monde hélas imparfait et sur un système comme Linux, cette période est plus ou moins bien suivie et le temps entre deux mesures peut être variable. Pour gérer cette variabilité, il est conseille de prendre comme dt la différence de date entre la mesure précédente et la mesure courante: dt = t - t' avec t' la date précédente de mesure. Cela nécessite bien sûr de mémoriser t'.

La fonction de variation de l'erreur est beaucoup trop complexe pour être représenter mathématiquement face à des phénomènes externes bien prédictibles. On se contentera alors d'utiliser des méthodes approchées pour calculer l'intégrale :

• méthode des rectangles : INT[0 → t] = INT[0 → t'] + e(t) dt
• méthode des trapèzes : INT[0 → t] = INT[0 → t'] + ( (e(t) - e(t') ) / 2) dt

Dans le même esprit, la dérivée peut être facilement approximée par : (e(t) - e(t') ) / dt

• Introduction